The Effects of Time on Polymers
Last month we briefly discussed the influence of temperature on the mechanical properties of polymers and reviewed some of the structural considerations that govern these effects.
Last month we briefly discussed the influence of temperature on the mechanical properties of polymers and reviewed some of the structural considerations that govern these effects. We noted that this behavior distinguishes plastic materials from metals and makes them inherently less predictable. This month we will start to cover the second dimension of the map that governs the behavior of these materials: time.
Knowing the effects of temperature on the load-bearing properties of a material is important, but the measurements are made over a short time scale. If we extend the time scale of the measurement process, we encounter a continuing change in the response of the material. If the material is under constant stress, we observe this continual change as an ever-increasing level of strain, known as creep or cold flow. If the material is under constant strain, we observe a decay in the stress required to maintain this strain. The two responses, while not precisely the same, are similar. And one of the ways that we express this behavior is using a quantity known as the apparent modulus.
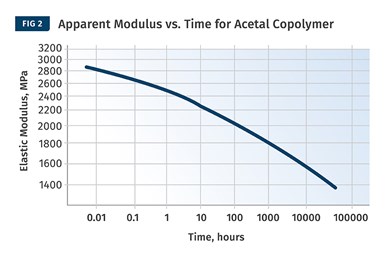
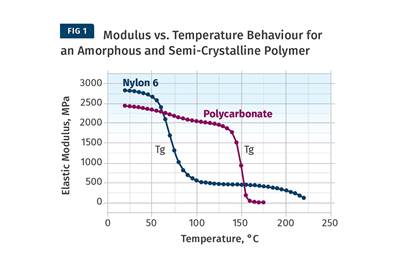
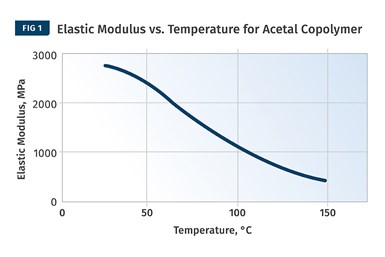
If you plot elastic modulus vs. temperature on a linear scale (Fig 1) and then plot apparent modulus as a function of time on a logarithmic scale (above), you’ll see that the shapes of the curves are very similar. Therefore, if you have information on the temperature-dependent behavior of a material, you can infer, at least in a semi-quantitative way, what will happen to that material over an extended time under constant stress.
The modulus of a material is expressed as the applied stress divided by the resulting strain. On a data sheet this usually is given for that limited region of the stress-strain curve where the two values are consistently proportional. As such, this value is the slope of the stress-strain curve in the linear region of the curve and is sometimes referred to as the tangent modulus or Young’s modulus.
Specific Stress and Secant Modulus
For some materials, a secant modulus is provided. This represents a straight line drawn from the origin to a particular point on the stress-strain curve such as 1% or 2%. This is most often done for materials like polypropylene and polyethylene. Since these polymers do not exhibit linear behavior at such high strains, the drawn line cuts the corner off the actual stress-strain curve and therefore the secant modulus will always be lower than the tangent modulus.
When a material is placed under a specific stress, the strain realized initially will be a function of the modulus of the material. If the stress is maintained, the strain will continually increase. Therefore, if we calculate the modulus an hour later it will appear to have declined. If we wait longer, say 1000 hr, the modulus will appear to have declined even further.
The actual stiffness of the material is not really decreasing. If we remove the stress from the material and then reapply that same stress again we find that the relationship we observed between stress and initial strain will be essentially the same. Consequently, the apparent modulus is just what it suggests; it is the apparent stiffness of the material based on a calculation made up of a constant stress and an ever-increasing strain. It is, therefore, a mathematical construct for talking about the effect of a constant stress on the manner in which strain increases over time.
Apparent and Tensile Modulus
As hard as it is to find continuous plots of modulus versus temperature, it is even more difficult to find continuous plots of apparent modulus as a function of time. Occasionally, a data sheet will provide a line item or two that probably look unfamiliar. They will refer to a property known as creep modulus and there will be a reference to a particular time. The accompanying table provides an example for an unfilled acetal copolymer.
The tensile modulus can be thought of as the representing the instantaneous or “zero-time” response of the material. The creep modulus values tell us something about how the material behaves if a constant stress is maintained. The increase in the strain is proportional to the ratio of the “zero-time” modulus and the creep modulus. So after 1 hr under constant stress, these values tell us to expect an increase in strain of approximately 12.7%. After 1000 hr the creep modulus predicts that the initial strain will have approximately doubled (2758/1352 = 2.04).
This brings to light an interesting and extremely important aspect of the behavior of viscoelastic materials. The same changes in modulus that can be brought about by increases in temperature can also be simulated by increasing the time scale of the measurement process without changing the temperature. A plot of elastic modulus versus temperature for this material shows that the modulus of the material will decline to 1352 MPa at a temperature of 89 C (192 F).
In other words, applying a constant stress at room temperature for 1000 hr produces the same response that would be observed instantaneously under the same stress at 89 C. This is an example of what is often referred to in treatments of viscoelastic materials as the time-temperature equivalence. Whatever can happen rapidly at an elevated temperature can also happen more slowly at a lower temperature. In this particular case, an increase of 66° C equals a time scale of 1000 hr under load.
If we plot elastic modulus vs. temperature on a linear scale and then plot apparent modulus as a function of time on a logarithmic scale, we find that the shapes of the curves are very similar (see Figs. 1 and 2). So if we have access to information regarding the temperature-dependent behavior of a material, we can infer, at least in a semi-quantitative way, what will happen to that material over an extended time period under constant stress. Using advanced techniques and the same dynamic mechanical analyzer that we employ to determine the temperature-dependent behavior of a material, we can establish quantitative relationships between time and temperature for any material over a wide range of conditions.
More importantly, because creep and stress relaxation proceed much more rapidly at elevated temperatures, we can leverage the time and temperature link to construct short-term experiments that allow us to make accurate predictions of long-term behavior without waiting for real-time results that might take years to obtain.
The only shortcoming of the apparent modulus measurements we have presented here is that they do not define the actual stress and strain at which the measurements are made. Modulus refers only to the ratio of stress to strain. Because plastic materials produce stress-strain curves that change slope considerably as they proceed from zero to the yield or break point, the picture is incomplete unless we define the applied stress. This is the third dimension needed to define the long-term load-bearing performance of a material. But before we tackle this dimension we have a little more to say about time. And we will cover that next month.
About the Author: Michael Sepe is an independent materials and processing consultant based in Sedona, Ariz., with clients throughout North America, Europe, and Asia. He has more than 45 years of experience in the plastics industry and assists clients with material selection, designing for manufacturability, process optimization, troubleshooting and failure analysis. Contact: (928) 203-0408 • mike@thematerialanalyst.com
Related Content
The Strain Rate Effect
The rate of loading for a plastic material is a key component of how we perceive its performance.
Read MoreHow to Get Rid of Bubbles in Injection Molding
First find out if they are the result of trapped gas or a vacuum void. Then follow these steps to get rid of them.
Read MoreFormulating LLDPE/LDPE Blends For Abuse–Resistant Blown Film
A new study shows how the type and amount of LDPE in blends with LLDPE affect the processing and strength/toughness properties of blown film. Data are shown for both LDPE-rich and LLDPE-rich blends.
Read MoreA Simpler Way to Calculate Shot Size vs. Barrel Capacity
Let’s take another look at this seemingly dull but oh-so-crucial topic.
Read MoreRead Next
The Effects of Temperature
The polymers we work with follow the same principles as the body: the hotter the environment becomes, the less performance we can expect.
Read MoreAdvanced Recycling: Beyond Pyrolysis
Consumer-product brand owners increasingly see advanced chemical recycling as a necessary complement to mechanical recycling if they are to meet ambitious goals for a circular economy in the next decade. Dozens of technology providers are developing new technologies to overcome the limitations of existing pyrolysis methods and to commercialize various alternative approaches to chemical recycling of plastics.
Read MoreLead the Conversation, Change the Conversation
Coverage of single-use plastics can be both misleading and demoralizing. Here are 10 tips for changing the perception of the plastics industry at your company and in your community.
Read More.jpg;width=70;height=70;mode=crop)