Materials: Cycle Time: Science vs. Rules of Thumb—Part 2
Understanding cooling—how a given material develops modulus as it solidifies—requires access to data that provides some insight into the relationship between modulus and temperature. Dynamic mechanical analysis is a helpful tool.
In June’s column, I discussed the often-cited connection between the deflection temperature under load (DTUL) for a given material and the appropriate temperature at which a part molded from that material can be ejected from the mold without exhibiting excessive distortion while cooling the rest of the way down to room temperature. Not everyone subscribes to this direct correlation. About a month ago I read an article that confidently told readers that a material must be cooled to a temperature equal to 80% of the DTUL in order to be successfully ejected from the mold. For the moment let’s set aside the question of where this “rule of thumb” came from and examine how the industry attempts to use these guidelines.
Usually the temperatures in the equations we use to calculate cooling time are given on the Celsius scale. If the DTUL of a material, such as a 40% glass-filled nylon 66, is given as 250 C, then a simple calculation gives us 80% of the DTUL as 200 C. But if we decide to use the Fahrenheit scale, then we convert 250 C to 482 F. When we perform the same calculation, we do not get quite the same result. Eighty percent of 482 F is 385.6 F, which converts to 196 C.
This may seem like a trivial difference, but the absurdity of using either of these scales becomes more evident when we lower the temperature to the point where the values become negative. We do not measure the DTUL of elastomers for the reasons mentioned in the previous article. But if we did, we would always obtain a value that is below room temperature and even below zero. In elastomers, we tend to refer to the temperature where the material starts to build modulus rapidly as the brittleness temperature, and it is actually associated with a very important transition that occurs in all polymers known as the glass transition.
Consider an elastomer like Santoprene 203-50, a TPV that has the highest hardness of any grade in this product line. The brittle- ness temperature of the material is given on the data sheet as -18.4 F, which converts to -28 C. If you take 80% of the Fahrenheit temperature you obtain a value of -14.7 F; for the Celsius scale, the value it is -22.4 C. Either way, the result is a higher temperature. And, by the way, -22.4 C equals -8.3 F, over 6° different from the result we obtain when calculating from the Fahrenheit scale. In addition, anyone who has ever molded this material knows that it does not have to be cooled to this temperature to be ejected from the mold. This conundrum will apply to any elastomer.
Physicists and chemists learned a long time ago that temperature is related to molecular mobility. The higher the temperature, the greater the mobility of the atoms or molecules in the material. Given that understanding, all properly designed equations that involve temperature use a scale where zero is associated with a cessation of translational motion. It is called absolute zero and the scale most often used is the Kelvin scale, which is the Celsius scale shifted by approximately 273°. It is possible to perform the same adjustment to the Fahrenheit scale, in which case the adjustment is approximately 459° and the resulting scale is referred to as the Rankine scale. At least if we used these scales, then when we took 80% of a given temperature on both scales we would end up with the same result.
Consider restating the calculation on the Kelvin scale for the glass-filled nylon. The value of 250 C now becomes 523 K, and 80% of this new value gives us 418.4 K or 145.4 C instead of the 200 C we calculated using the Celsius scale. A similar shift would occur if we changed from Fahrenheit to Rankine. The value of 482 F would become 941 R, and 80% of this value gives 752.8 R or 293.8 F, which is equal to 145.4 C to within a tenth of a degree.
So by converting to the absolute scale we get rid of two issues. First, there is no more built-in error in the calculation of a percentage depending upon the scale we choose. Second, we avoid the problem of calculating a value that goes to a higher temperature when we take a percentage of a published thermal property. But then we might need to reformulate our rule of thumb of 80%, because suddenly our ejection temperature has dropped by 55 C. Does that mean we have been running too fast all these years?
Fortunately, this little exercise in correcting our equations is not important, because the notion that a simple percentage of a property that is poorly defined (which DTUL do we use?) and has no value as an engineering property can be used to calculate cycle time is ridiculous. Cooling a material to an ejectable temperature is all about how a given material develops modulus as it solidifies. To understand this, it is necessary that we have access to data that provides some insight into the relationship between modulus and temperature. For this we use an analytical technique known as dynamic mechanical analysis (DMA).
DMA provides us with an immense amount of information about material properties. But for purposes of this discussion let’s focus on one of the simplest and most easily understood outputs from the instrument: the elastic modulus as a function of temper- ature. We know that as a material cools it becomes stiffer; the modulus of the material increases. What we often are not aware of is how that modulus increase takes place with a specific change in temperature. This is where DMA is very helpful.
Figure 1 shows plots of elastic modulus for an amorphous polymer, polycarbonate, and a semi-crystalline polymer, nylon 6. In both cases the materials are unfilled. Typically, these results are generated by heating a sample of the material at a particular rate and continuously monitoring the elastic modulus. It is readily apparent that the relationship between modulus and temperature differs significantly depending upon the structure of the material. Amorphous polymers such as polycarbonate experience one significant step change in modulus with increasing temperature. This is the glass transition, and it results in a nearly complete loss in stiffness as the material passes through this relatively narrow temperature range.
Semi-crystalline polymers go through a more complicated process. They exhibit a relatively significant reduction in modulus as they pass through the glass transition. But unlike amorphous polymers, the decline is not complete. Instead, a new plateau is achieved that is related to the contribution from the crystal structure. This plateau is maintained until the material approaches the temperature at which these crystals melt.
Engineers designing parts, especially for elevated-temperature service, should read these curves from left to right, watching for temperature regions where significant changes in modulus occur. Knowing, for example, that the modulus of an unfilled nylon 6 at 100 C is only 20% of the modulus at room temperature can help the design engineer make sound decisions about the geometry of the part if it is to manage stress at this higher temperature. Processors, however, should read these curves from right to left, because this describes how the material increases in stiffness as it cools. There will be small offset in the temperatures associated with these important transitions, but the general behavior will be the same for both heating and cooling.
Next month, I will look more closely at these curves and hopefully put to rest the notion that deflection temperature under load, or some percentage of that property, however precisely it is calculated, has anything to do with the temperature at which a part can be demolded.
ABOUT THE AUTHOR: Mike Sepe is an independent, global materials and processing consultant whose company, Michael P. Sepe, LLC, is based in Sedona, Ariz. He has more than 40 years of experience in the plastics industry and assists clients with material selection, designing for manufacturability, process optimization, troubleshooting, and failure analysis. Contact: (928) 203-0408 • mike@thematerialanalyst.com.
Related Content
Thermoplastic Elastomers With Recycled Content for Automotive Applications
Avient announced new grades of TPE to meet demand for recycled content.
Read MoreResins & Additives for Sustainability in Vehicles, Electronics, Packaging & Medical
Material suppliers have been stepping up with resins and additives for the ‘circular economy,’ ranging from mechanically or chemically recycled to biobased content.
Read MoreMulti-Purpose TPV with Post-Industrial Recycled Content
Teknor Apex’s new Sarlink R2 3180B TPV offered with 25% PIR content.
Read MoreFast-Cycling Selective Laser Sintering System
Nexa3D announced the QLS 260 for metal and polymer production.
Read MoreRead Next
Cycle Time: Science vs. Rules of Thumb, Part 1
What temperature must the polymer reach so the part can be ejected from the mold? Here, more than for any other variable, ‘rules of thumb’ unfortunately prevail.
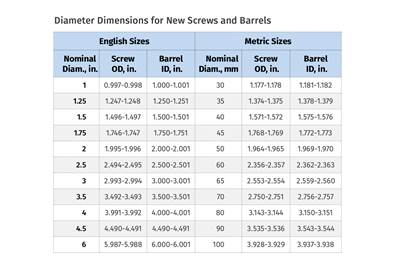
Read MoreTroubleshooting Screw and Barrel Wear in Extrusion
Extruder screws and barrels will wear over time. If you are seeing a reduction in specific rate and higher discharge temperatures, wear is the likely culprit.
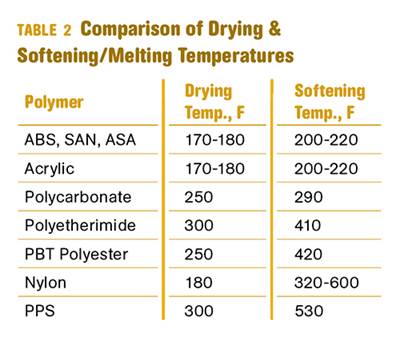
Read MoreWhy (and What) You Need to Dry
Other than polyolefins, almost every other polymer exhibits some level of polarity and therefore can absorb a certain amount of moisture from the atmosphere. Here’s a look at some of these materials, and what needs to be done to dry them.
Read More
.jpg;width=70;height=70;mode=crop)



















.png;maxWidth=300;quality=90)