Water-bath length usually ends up being decided not by a theoretical approach or practical experience, but by how much space is left over on the production floor.
In strand pelletizing, determining how long the water bath should be is probably one of the more overlooked matters in the initial system design. The length of a water bath usually ends up being decided not by a theoretical approach or practical experience, but by how much space is left over on the production floor. This can lead to processing issues if the water bath is too short, or wasted space if the water bath is too long.
Some processors are fortunate to have prior experience to give them an indication of how long a new water bath should be. Others should consider using a theoretical approach based on unsteady-state heat-transfer equations to come to a theoretical length for a water bath. These theoretical methods have been explored by many extrusion experts over the years. The purpose of this article is to provide a shortcut to get you in the ballpark of how long your water bath should be.
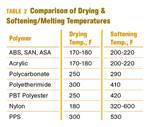
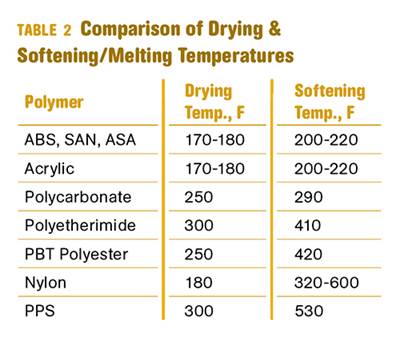
First, you need to know your line speed. Once you have that, you need to find a Heisler chart like the one in Fig 1. There are different Heisler charts for different extruded shapes, so make sure you pick the correct one. These Heisler charts are readily available via Google searches. Figure 1 is a Heisler chart for a cylinder, much like the strands in a strand pelletizing operation.

FIG 1 You can find all types of Heisler charts on the internet, so it’s important to pick the right one for your calculations. This one can be used for strand pelletizing.
Those blue lines are all inverse Biot numbers (a dimentionless quantity used in heat-transfer calculations) for the object you’re trying to cool. To get a ballpark number for how long your water bath should be, use the blue line designated with a 0. Why? Because polymers are generally poor thermal conductors, strands are thin, and you have a steady flow of water going through your water bath.
If one of those situations doesn’t apply, you’ll have to find the hydraulic diameter of your water bath; Reynolds, Prandtl, and Nusselt numbers for the water cooling your strands; and the convective heat-transfer coefficient to determine the right line to use. If that sounds scary, just use the blue line designated with a 0.
Then we calculate the approach temperature Θ*. This is basically the ratio of the temperature of your plastic coming out of the die head and the temperature you want for the plastic before it gets cut into pellets. If you need guidance on what your desired plastic temperature should be, you can search online for “softening points” of the polymer you are interested in and subtract 20° F from that. For polypropylene, 192 F has been found to work well, but the desired temperature depends on the particular polymer and pelletizer capabilities. For example:
Θ* = (Tplastic, desired – Twater)/(Tplastic, initial – Twater) =
(192 F – 78 F)/(420 F – 78 F) = 0.31
Now with that red line number 0 and approach temperature, we can determine our Fourier number from the Heisler chart. You take your approach temperature Θ* on the left and go to the right until you hit the blue line that represents your inverse Biot number. As shown in Fig. 2, the Fourier number is around 0.32.
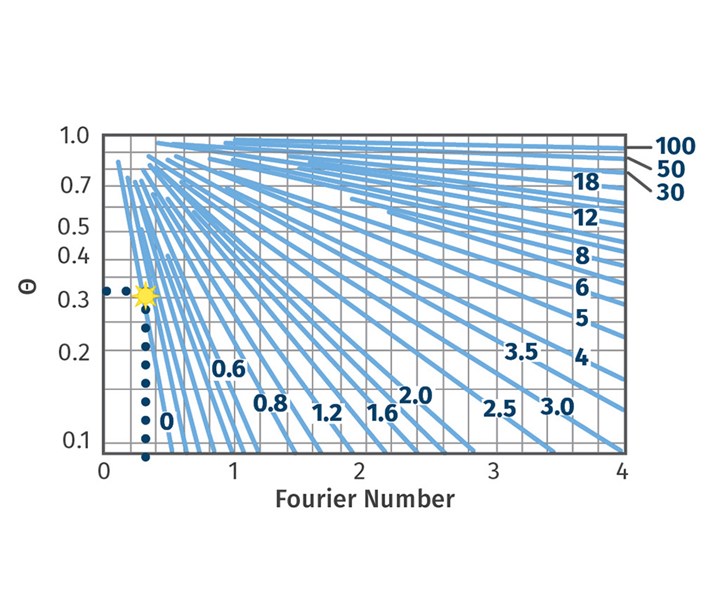
FIG 2 With the blue line numbered 0 and approach temperature, you can determine your Fourier number from the Heisler chart. You take your approach temperature Θ* on the left and go to the right until you hit the line that represents your inverse Biot number. As shown here, the Fourier number is around 0.32.
With the Fourier number, we can now calculate the time required for the plastic strands to reach the desired temperature. I used PP in this example, with a radius of the PP strand I’m trying to cool at 0.00239 m (which I got from my die hole diameter).
α = thermal diffusivity of PP = 9.6 x 10-8 m2/sec
t = (F0 × r02)/α = (0.32 x 0.00239 m2)/(9.6 × 10-8 m2/s) = 18.77 sec
Now that we know the time required in the water bath, we can use the line speed calculated earlier to calculate the predicted water bath length.
Lwater bath = t × Line Speed = 18.77 sec × 2.500 ft/sec = 47 ft
If your calculated water bath is longer than the space you have in your facility, you could attempt the following:
• Purchasing or renting a chiller to lower the incoming water temperature if your cooling-water temperature is above 72 F.
• Using spray bars to take advantage of evaporative cooling to cool the strands more.
• Adjusting water-bath roller setup to make multiple passes in the water bath either length-wise or height-wise.
• Using multiple water baths instead of a single bath.
Remember that this is a method just to get you in the ballpark of how long your water bath should be. In the interest of full disclosure, there are some drawbacks to utilizing this technique, as it ignores the effects of these factors:
• The number of strands;
• Crystalline polymers’ heat of fusion as they transition from molten to solid;
• The changing values of constants (i.e. heat capacity of polymer) as temperature changes;
• The number of times strands leave and re-enter water bath;
• Use of additives or fillers and their effects on physical properties.

FIG 3 When a plastic strand enters the water bath, it heats the water around it or forms a steam jacket. As a result, the water bath is trying to cool that hot water layer before it can cool the strand. This delays the cooling effect of the water bath. In the absence of any turbulence, you’re basically left with trying to cool hot plastic strands with warm water--a sub-optimal cooling situation. (Photo: Conair)
I recommended that you verify first-hand the thermophysical properties of the plastic you’re trying to cool, or else you may be unpleasantly surprised when your plastic doesn’t behave like textbooks or technical articles tell you it should.
EDITOR’S NOTE: This article is based on a presentation the author made during Plastics Technology’s Extrusion 2019 Conference, which was held in September in Rosemont, Ill.
About the Author: Bruce Spencer III is a process engineer for Sabic in Bay St. Louis, Miss. He has held various positions in the plastics industry since 2014, including EHS and production roles. He holds a BE in chemical engineering. Contact: (228) 466-3023; bruce.spencer@sabic.com
Read Next
Lead the Conversation, Change the Conversation
Coverage of single-use plastics can be both misleading and demoralizing. Here are 10 tips for changing the perception of the plastics industry at your company and in your community.
Read MoreWhy (and What) You Need to Dry
Other than polyolefins, almost every other polymer exhibits some level of polarity and therefore can absorb a certain amount of moisture from the atmosphere. Here’s a look at some of these materials, and what needs to be done to dry them.
Read MoreProcessor Turns to AI to Help Keep Machines Humming
At captive processor McConkey, a new generation of artificial intelligence models, highlighted by ChatGPT, is helping it wade through the shortage of skilled labor and keep its production lines churning out good parts.
Read More