The Effects of Temperature
The polymers we work with follow the same principles as the body: the hotter the environment becomes, the less performance we can expect.
Four to five times a year, I like to hike in the Grand Canyon. Anyone who does this type of thing has discovered that a 10-mile ascent from the river to the rim is more easily accomplished in early spring than in the middle of summer. As it turns out, when placing the body under significant stress, the chances that things will go well are influenced by temperature.
The polymers we work with follow the same principles. The hotter the environment becomes, the less performance we can expect.
Engineers classically trained in materials know metals. Consequently, they are accustomed to a level of certainty where temperature-dependent behavior is concerned that polymers do not provide. Even a relatively low-performing metal such as aluminum has essentially the same mechanical properties between room temperature and 250-300°C, and even when approaching the melting point, retention can be as high as 80% of room-temperature performance. This level of consistency is even better for materials like copper, brass, and steel, where the melting points are higher. This certainty is aided by the fact that the building blocks for metallic substances are small and readily organize into a well-defined and predictable crystal structure.
That is not the case for polymers. The individual molecules that make up polymeric materials are very large and have an extended chain-like shape that results in an entangled structure. This entanglement is beneficial in some respects. The relatively high levels of elongation that most polymers exhibit without breaking are due in large part to chain entanglement. However, this entanglement also restricts the freedom required at a molecular level to organize into crystals. Consequently, no polymer under normal processing conditions is fully crystalline, and some polymers do not crystallize to any significant degree.
Changes in Temperature
This lack of a predictable and repeatable structure gives rise to a situation where changes in temperature always influence the mechanical properties of these materials. This phenomenon can be captured by performing mechanical tests at various temperatures on any given material. One of the simplest ways to capture the load-bearing properties of a material over a wide range of temperatures involves a method known as dynamic mechanical analysis (DMA). This technique can measure so many aspects of polymer behavior that whole books have been devoted to the topic. However, for our purposes we can focus on one small aspect: the ability to measure the elastic modulus of a material as a function of temperature.
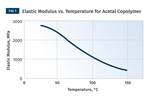
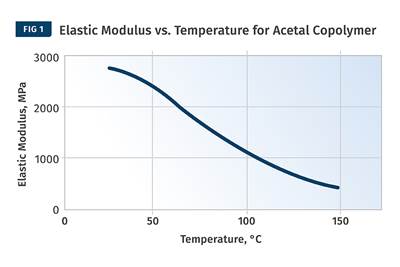
Figure 1 provides a modulus vs. temperature plot for two well-known and commonly used polymers; nylon 6 and polycarbonate (PC). Both of the materials tested are unreinforced. Nylon 6 is a semi-crystalline polymer, while PC is amorphous, and the results shown here represent typical behavior for these two classes of materials. At room temperature the elastic modulus for both materials agrees with the tensile modulus quoted on the data sheet to within 2-3%. But while most data sheets provide little or no information on the effect of temperature on properties, the plots in Fig. 1 give a complete map of the temperature-dependent behavior for the two materials.
No polymer under normal processing conditions is fully crystalline, and some polymers do not crystallize to any significant degree.
Amorphous PC exhibits only one transition temperature, known as the glass-transition temperature (Tg). This represents the temperature at which the individual polymer chains become sufficiently mobile at a molecular level to move independently despite the fact that they remain entangled. Structurally, this event can be likened to a softening temperature, and for engineering purposes the material loses all load-bearing properties as it passes through this transition. Between room temperature and the onset of the glass transition, the modulus of PC is relatively consistent, declining by approximately 20% between room temperature and 135°C, a value that happens to agree well with the deflection temperature under load (DTUL) that is provided on most data sheets. However, between room temperature and the DTUL, most data sheets provide little guidance on the effects of temperature on load-bearing capabilities.
Semi-Crystalline Nylon 6
The behavior of the semi-crystalline nylon 6 is somewhat different than that of the amorphous PC. Nylon 6 is referred to as semi-crystalline because, like all polymers in this class, it consists of a structural mix of crystalline and amorphous regions. As the temperature increases, the amorphous regions become mobile and this mobility is again signaled by the glass transition. This occurs between 50°C and 100°C with a midpoint near 70-75°C, and as a result the modulus declines to about 20% of its room-temperature value. But it does not fall to zero like PC does because of the presence of the crystalline structure.
This organized structure preserves a reduced level of performance that is maintained until the temperature rises to the melting point of the nylon crystals, or about 220-225°C. All amorphous polymers follow a temperature response that is similar to that of PC. The only difference between various amorphous polymers such as ABS, PVC, PC, and polysulfone is the glass-transition temperature. Nylon 6 serves as a model for the temperature-dependent behavior of all semi-crystalline polymers. The distinguishing features among semi-crystalline polymers include the glass-transition temperature, the melting point, and the degree of decline in modulus associated with the glass transition. For most unfilled, semi-crystalline polymers this decline will be 60-90% of the pre-Tg modulus.
The more crystalline the polymer structure is, the smaller the modulus decline through Tg.
It is important to emphasize that the Tg and the melting point (Tm) are fundamental properties for each polymer. We can reduce the effect that the Tg has on the elastic modulus of a semi-crystalline polymer by adding fillers and reinforcements. We can achieve similar benefits in amorphous polymers at temperatures below the Tg. However, the transition temperatures do not change. The Tg (for amorphous polymers) and the Tm (for semi-crystalline polymers) represent the upper limit at which the polymer can operate in an application environment even over a very short time frame. Short in this case may be defined in minutes, not hours, days, or weeks.
Stress-Strain Curves
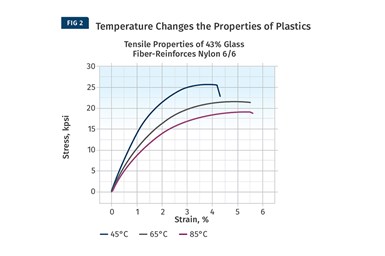
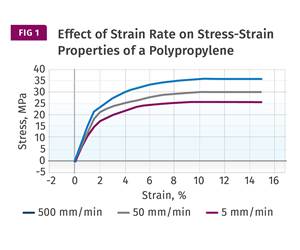
While DMA provides a complete map of the behavior of modulus as a function of temperature, it tells us nothing about the actual strength of the material. For this we need to refer to stress-strain curves and examine the relationship between stress and strain as a function of changes in temperature (see Fig. 2 comparing curves for a 43% glass fiber-reinforced nylon 66).
Despite the fact that almost half of the compound is made up of the non-polymeric glass fiber, the shape of the stress-strain curve changes significantly. In general, strength and stiffness decrease with increasing temperature while elongation at break, a good relative indicator of ductility, increases. While all three of these curves are relatively close to room temperature, the performance of the material declines to a significant degree compared with the values provided on the data sheet. At 85°C the yield strength of this material is less than 60% of the room-temperature value listed on the data sheet.
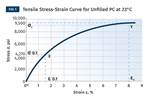
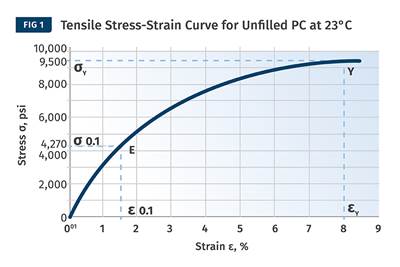
Also, the data sheet only talks about particular points on the curve. Yield stress and strain represent a single coordinate on the continuum of the stress-strain curve, and the modulus is simply the slope of this curve in the region where the two quantities are proportional.
In order to accurately model the structural behavior of a material, it is important to know the shape of the stress-strain curve at the application temperature. This includes the point on the curve where the relationship between stress and strain becomes non-linear; the so-called proportional limit. While strains at yield typically range from 3% to 10% for most thermoplastics, the strain at the proportional limit rarely exceeds 1% and for many materials it is less than 0.5%.
Sixty years ago, plastics were often considered cheap substitutes for wood, metal, and glass. The markets they served often did not make significant demands upon the load-bearing aspects of the materials and the effects of temperature variation were of minimal concern. But today plastic materials are used in a wide variety of demanding application environments where a high degree of reliability is expected over a wide range of temperatures for extended periods of time. Our understanding of the properties of these materials must catch up with these demands. Next month we will discuss time and strain rate, two aspects of a second factor that is critical to understanding the mechanical properties of polymers.
About the Author: Michael Sepe is an independent, global materials and processing consultant whose company, Michael P. Sepe LLC, is based in Sedona, Arizona. He has more than 45 years of experience in the plastics industry and assists clients with material selection, designing for manufacturability, process optimization, troubleshooting and failure analysis. Contact: 928-203-0408 • mike@thematerialanalyst.com.
Related Content
Polyethylene Fundamentals – Part 4: Failed HDPE Case Study
Injection molders of small fuel tanks learned the hard way that a very small difference in density — 0.6% — could make a large difference in PE stress-crack resistance.
Read MoreThe Importance of Melt & Mold Temperature
Molders should realize how significantly process conditions can influence the final properties of the part.
Read MoreThe Strain Rate Effect
The rate of loading for a plastic material is a key component of how we perceive its performance.
Read MoreUnderstanding Strain-Rate Sensitivity In Polymers
Material behavior is fundamentally determined by the equivalence of time and temperature. But that principle tends to be lost on processors and designers. Here’s some guidance.
Read MoreRead Next
The Effects of Time on Polymers
Last month we briefly discussed the influence of temperature on the mechanical properties of polymers and reviewed some of the structural considerations that govern these effects.
Read MoreThe Effects of Stress on Polymers
Previously we have discussed the effects of temperature and time on the long-term behavior of polymers. Now let's take a look at stress.
Read MoreThe Strain Rate Effect
The rate of loading for a plastic material is a key component of how we perceive its performance.
Read More.jpg;width=70;height=70;mode=crop)