EXTRUSION: Cooling: The Critical Function in Extrusion
Figuring out how much cooling your process needs is complicated. But there are ways to approximate.
Every extruded shape must be cooled to a temperature at which it will maintain its desired dimensions, using a cooling medium such as a gas, liquid, or contacting metal surface. Regardless of the extruded shape or the cooling medium, removal of the heat to hold the dimensions is as important a process as adding the heat during extrusion to make the polymer flow.
Many processors expect cooling requirements to be based simply on output, or pounds per hour. This often leads to false expectations when product shape and/or thickness (gauge) are changed. Because of the low thermal conductivity of polymers, the cooling limit is often determined by heat transfer through the polymer itself, rather than the cooling medium, except for very thin shapes. In the case of thicker shapes, predicting the cooling rates can be quite complicated.
A calculation for determining the heat-transfer in your process can be obtained with use of the heat-transfer equation. This gives you the overall heat-transfer coefficient, which is the heat transfer between the polymer and the cooling medium.
Although there are various published data for overall heat-transfer coefficients between polymers and the cooling medium, they are usually not specific to your operation and should be determined experimentally. By substituting an actual extrusion condition in this simple formula, your overall heat-transfer coefficient (Uo) can be determined:
Q = U₀A₀ΔT₀ when:
Q = The rate of heat of transfer (Btu/hr) = lb/hr × specific heat × (melt temperature minus exit temperature).
U₀ = The overall heat-transfer coefficient
(Btu/hr-ft2 -°F).
A₀ = The overall cross-sectional area for heat transfer (ft2) = perimeter x ft/hr.
ΔT₀ = The overall temperature differential (°F) = melt temperature minus exit temperature.
Once you know the overall heat-transfer coefficient you can substitute actual data into this formula to estimate different outputs and/or differential temperatures for the same cross-section.
However, when estimating a different cross-section (dimensions, shape) or a different polymer, this calculation cannot be used. The cooling calculations become much more complicated because the polymer’s thermal properties, rather than the cooling medium, often limit the transfer of heat.
You can use a Biot number (Bi), which compares the ratio of the internal heat resistance to the external heat resistance at the surface; it will indicate whether the internal or external heat transfer is the limiting parameter in cooling. A product with a Bi smaller than 1 has little internal temperature gradient and cools as a uniform body. As the Bi increases above 1 the part has a progressively larger thermal gradient in the shape as it cools. Using a Bi gives a rapid and simple analysis as to whether the internal heat transfer through the polymer shape or the external cooling medium will dominate the cooling process.
Biot Number (Bi) = (Heat-transfer coefficient × half the thickness)/thermal conductivity
Heat transfer coefficient=U₀
Thickness=Ft
Thermal conductivity=Btu/Ft-Hr-°F
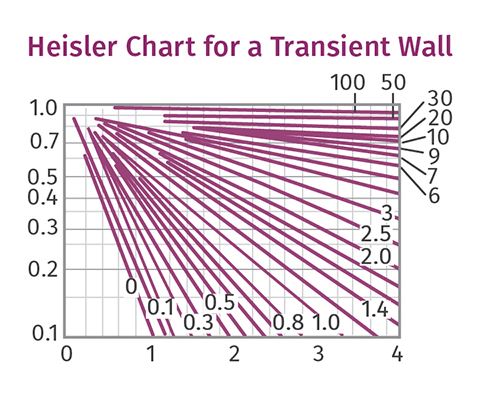
To determine whether a different polymer shape or thickness will have a significant effect on the cooling time, you need to know the effect of the thermal heat transfer in the polymer itself. An approximate approach is to refer to a Heisler chart to or to an online calculator to determine the Fourier number (τ). With the Fourier number, the effect of the internal heat-transfer coefficient can be calculated and separated from the external heat-transfer coefficient.
Fourier number (τ) = (K/Cs × S.W. × t)/L²
This is done by locating the Biot “curve” and the dimensionless temperature (θ) on the Heisler chart.
(θ) = Final temperature at center - coolant temperature/Initial temperature -
coolant temperature
The Fourier number is where (θ) and the Bi curve intersect. It is made up by the polymer’s thermal conductivity (K), specific heat (Cs), and specific weight (S.W.), plus the distance (L) to the center of the extrudate shape, and the (t) time for cooling. Time can be determined by substitution of the other variables.
Fourier numbers less than 0.2 generally should not be used. Complete directions for use and interpolation of the Heisler charts for several shapes can be found online. Adjustments can be made to accommodate cooling from one side, as with pipe, bottles or blown film. The Heisler chart can approximate cooling rates without working through extensive experimental data and complex calculations that require a computer program and an advanced understanding of advanced mathamatics.
Related Content
Multicoupling Range Extended
Hasco‘s quick-connect system for multiple cooling circuits has added U.S., French and HT versions.
Read MoreImprove The Cooling Performance Of Your Molds
Need to figure out your mold-cooling energy requirements for the various polymers you run? What about sizing cooling circuits so they provide adequate cooling capacity? Learn the tricks of the trade here.
Read MoreSystem Offers 'Lights Out' Mold-Channel Cleaning & Diagnostics
New system automatically cleans mold-cooling lines—including conformal channels—removing rust and calcium, among other deposits, while simultaneously testing for leaks, measuring flow rate and applying rust inhibitor.
Read MoreTroubleshooting Leaky Temperature-Control Units
Learn the causes, symptoms and remedies for TCU leaks to keep these vital contributors to plastics processing up and running longer and more efficiently.
Read MoreRead Next
Why (and What) You Need to Dry
Other than polyolefins, almost every other polymer exhibits some level of polarity and therefore can absorb a certain amount of moisture from the atmosphere. Here’s a look at some of these materials, and what needs to be done to dry them.
Read MoreUnderstanding Melting in Single-Screw Extruders
You can better visualize the melting process by “flipping” the observation point so that the barrel appears to be turning clockwise around a stationary screw.
Read MoreLead the Conversation, Change the Conversation
Coverage of single-use plastics can be both misleading and demoralizing. Here are 10 tips for changing the perception of the plastics industry at your company and in your community.
Read More
.jpg;width=70;height=70;mode=crop)












.png;maxWidth=300;quality=90)