TOOLING: Balancing the Heat Budget In Injection Molds
Basic formulas for how much heat you must pull out of the mold to achieve a set cycle time
There are several reasons to be interested in the flow of energy into and out of injection molds. This balance of energy flow (the heat budget) is the basis for determining sufficiency of cooling circuits in an existing mold and for designing new tooling. This information can also be used to determine required size and capacity for portable and central coolant delivery systems. The following will introduce and explain the polymer science and simple calculations used to determine heat flows and balance the heat budget for any mold.
FIRST, THE PHYSICS
To begin, we will dust off the books and talk a bit about the nature of energy and materials. Many materials can exist in more than one state or phase. We experience this daily with water, which we often see as vapor (clouds and steam), liquid, or solid. To cause a change from one state to another, heat must be added or removed.
It is very interesting that during the phase change the temperature of the material remains constant. We all know water freezes at 32°F and boils at 212°F under standard conditions. The heat added or removed during the phase change is called latent (hidden) heat. Sensible heat is what we call the heat that changes the temperature of a substance.
An example of this is heating water at room temperature to boiling. The water will increase in temperature steadily until it boils. Then the temperature will stay at 212°F (at sea level) as it changes to steam, even as heat is steadily applied. Cooling water to freezing works just the same, the temperature holding at 32°F until freezing is complete. Remember, latent heat changes the state (or phase) of a substance without changing its temperature, and sensible heat changes only the temperature.
As we progress to a quantitative discussion about energy, we will employ the familiar British Thermal Unit (Btu), defined as the amount of energy required to heat 1 lb of distilled water 1° F. Another way of saying this is that water has a heat capacity of 1 Btu/lb-°F. As an interesting aside, water has the highest heat capacity among common substances, making it a very useful heat-transfer medium.
THE CONNECTION WITH POLYMERS
So what does all this have to do with plastics? Calculating the energy required to heat and cool a polymer during processing uses all the energy principles and units we have just introduced. However, an important difference exists between amorphous and semi-crystalline polymers. Semi-crystalline materials have a latent heat component that must be added during heating and removed during cooling to “thaw and re-freeze” the crystalline part of the molecular structure.
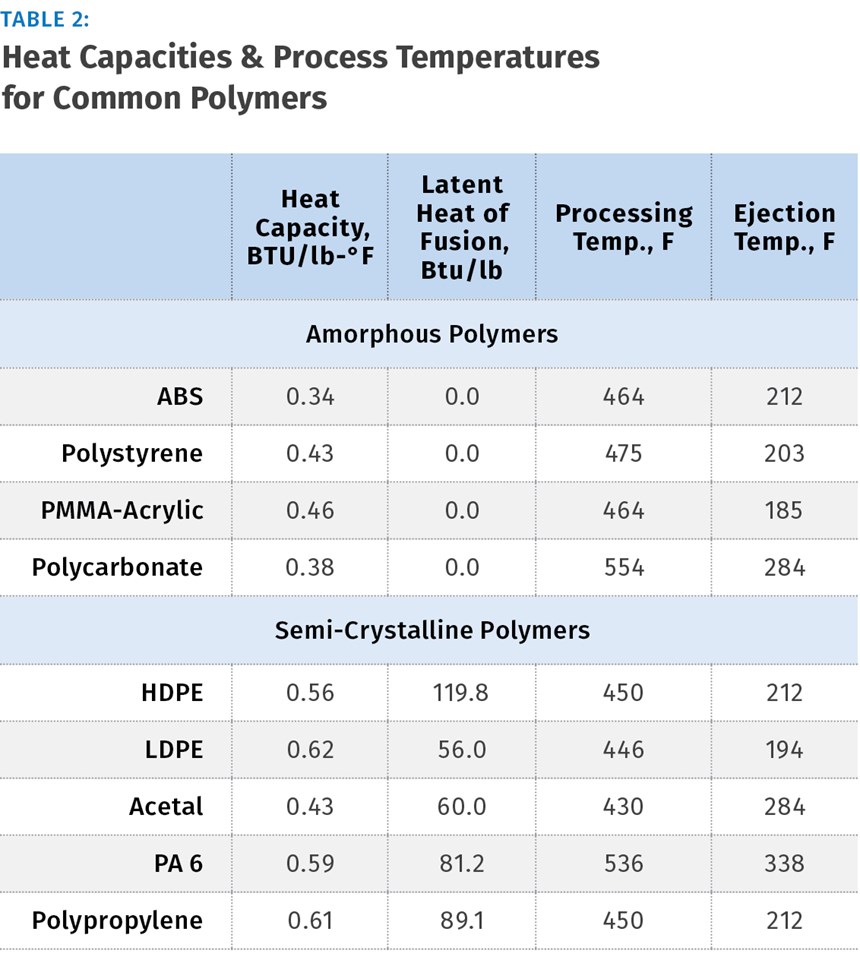
It is called Latent heat of Fusion and its units are Btu/lb. Amorphous polymers, of course, do not have the crystalline content and thus do not have a latent heat value. Table 2 shows heat capacity and latent heat of fusion values as well as some generic processing and ejection temperatures for common materials. Examples below will demonstrate how to perform energy calculations with both categories of polymers.
Using the data in Table 1 (plus a few assumptions), we can begin to perform several interesting and useful energy calculations. We can calculate the energy required to heat a material from room temperature to processing temperature, either per shot or per pound of material. We can also calculate energy flow rates into a mold or from a mold during part cooling.
AMORPHOUS MATERIALS CALCULATIONS
For simplicity we will begin with an amorphous material, polystyrene, and let’s say we are heating the material from room temperature at 80°F to a processing temperature of 475°F. Our shot weighs 0.25 lb (including conventional runner) and the cycle time is 12 sec. First we will calculate energy/lb using the expression (see Table 1 for definitions of each symbol):
Elb = W x ΔT x C
We are heating the material from 80°F to 475°F, thus:
ΔT = 475 F-80 F = 395° F.
Since we first want to calculate energy added per pound of material, we use 1 lb as the shot weight. From Table 1 we find the heat capacity of PS is 0.43 Btu/lb.-°F. Next we insert all the values into the expression as follows:
Elb = 1 lb x 395° F x 0.43 Btu/lb-°F = 169.9 Btu/lb of material
Next, let’s calculate the energy per shot using the same expression, but substituting our assumed shot weight of 0.25 lb to get the following result:
Eshot = 0.25 lb/shot x 395° F x 0.43 BTU/lb-°F = 42.46 Btu per shot
It is also interesting to calculate the heat flow in Btu/hr of heat input to the mold based on the above Btu/shot value. For this we need only to multiply Btu/shot by shots/hr (SPH) as follows:
Using our assumed cycle time,
SPH =3600 sec/hr ÷ 12 sec/cycle = 300
Energy flow into mold:
Q = 42.46 Btu/shot x 300 shots/hr = 12,738 Btu/hr
SEMI-CRYSTALLINE MATERIAL CALCULATIONS
In our next example we will calculate energy flow into an 8-cavity mold running a fairly thick, reuseable polypropylene food-storage container with a shot weight of 0.78 lb and cycle time of 16 sec. From Table 2 we select the heat capacity value of 0.61 Btu/lb.-°F, and latent heat of fusion value of 89.1 Btu/lb, the processing temperature of 450°F, and again a room temperature of 80°F.
The calculation method will be the same as for PS except we must include the latent heat with PP. Notice that the latent heat units are Btu/lb, thus the latent heat value depends only on weight, and not temperature. It will be interesting to compare Btu/lb heating from room to processing temperatures for the two materials. Thus, for PP we will begin with energy/lb using the following expression:
Elb = W x ((ΔT x C) + LF)
ΔT = 450 F-80 F = 370° F
Elb = 1 lb x ((370 x 0.61)+ 89.1) = (225.7+ 89.1) = 314.8 Btu/lb
Notice that even though the processing temperature for polystyrene is higher (475°F), PP requires nearly double the heat to reach processing temperature due to the latent heat that must be added to melt the crystalline structure.
Next we will calculate the energy flow rate for our PP part:
Eshot = 0.78 lb x ((370 x 0.61) + 89.1) =
0.78 x ((225.7+ 89.1) = 0.78 x 314.8 = 245.5 Btu/shot
Next we can calculate energy flow just as before, using
Q = BTU/shot x SPH
SPH = 3600 sec/hr ÷ 16 sec/cycle = 225
Q = 245.5 Btu/shot x 225 SPH = 55,238 Btu/hr
RULES OF THUMB & COOLING
One can find rules of thumb suggesting that the mold-cooling circuits should be capable of removing approximately 60% of the energy input to a mold like we have just calculated. Our studies indicate that while it is simple to estimate energy input to a mold, the various paths of heat removal are more complex and depend on several factors.
Conventional machined cooling circuits with liquid coolant normally do most of the cooling, but a heated mold can transfer significant heat to machine platens by conduction and also to the surroundings by radiation and natural convection. A ceiling fan placed directly above a molding machine can influence the heat-transfer balance and temperature of a mold. And don’t forget the significant heat remaining in the ejected parts and runner.
Another approach to estimating the cooling needs of a mold is to perform a calculation based on the difference between processing and ejection temperatures. I like this method because one can use a resin producer’s recommended processing and ejection temperatures—or better still, use experienced-based values you know and trust.
To illustrate, we will continue with the properties and values for our PP container. The major difference is that we have no need to calculate the heat added to the material to reach processing temperature. Instead, we can directly calculate cooling energy based on changing the temperature of the molded parts (and runner if applicable) from processing to ejection temperature.
One additional factor to consider is that the material may not be 100% crystallized in the part’s interior when the parts are ejected. You may have experienced this condition by feeling parts “heating up” to the touch after ejection. (Such “reheating” of parts after demolding can also occur if there are thick sections that remain hotter in the center than the frozen skin when the mold opens.) The degree of crystallization in the mold depends primarily on mold temperature and cooling capability. We will assume our parts are 60% crystallized when ejected and use a corrected latent heat value of 0.6 x 89.1 or 53.5 Btu/lb in our calculation.
To continue with our calculation, select processing and ejection temperatures for PP from Table 1:
Ecooling = W((ΔT x C) + LF)
Cooling ΔT is processing temperature minus ejection
temperature = 450-212 F = 238 °F.
Ecooling = 0.78 lb x ((238 x 0.61) + 53.5) =
0.78 x (145.2 + 53.5) = 155 Btu/shot
Qcooling = Ecooling x SPH = 155 Btu/shot x 225 SPH =
34,868 Btu/hr.
We can see that these calculations are fairly simple and straightforward. For best accuracy, use measured melt temperature as the processing temperature. The values provide a solid basis for evaluation of existing mold-cooling circuits or for designing cooling circuits for a new mold. They are also useful for estimating chiller capacities and water pumping capacity. In Part 2 we will explore water-cooling factors in balancing the heat budget.
Related Content
Improve The Cooling Performance Of Your Molds
Need to figure out your mold-cooling energy requirements for the various polymers you run? What about sizing cooling circuits so they provide adequate cooling capacity? Learn the tricks of the trade here.
Read MoreHow to Optimize Pack & Hold Times for Hot-Runner & Valve-Gated Molds
Applying a scientific method to what is typically a trial-and-error process. Part 2 of 2.
Read MoreBack to Basics on Mold Venting (Part 1)
Here’s what you need to know to improve the quality of your parts and to protect your molds.
Read MoreBest Methods of Molding Undercuts
Producing plastics parts with undercuts presents distinct challenges for molders.
Read MoreRead Next
Lead the Conversation, Change the Conversation
Coverage of single-use plastics can be both misleading and demoralizing. Here are 10 tips for changing the perception of the plastics industry at your company and in your community.
Read MoreUnderstanding Melting in Single-Screw Extruders
You can better visualize the melting process by “flipping” the observation point so that the barrel appears to be turning clockwise around a stationary screw.
Read MoreWhy (and What) You Need to Dry
Other than polyolefins, almost every other polymer exhibits some level of polarity and therefore can absorb a certain amount of moisture from the atmosphere. Here’s a look at some of these materials, and what needs to be done to dry them.
Read More