Cycle Time: Science vs. Rules of Thumb, Part 1
What temperature must the polymer reach so the part can be ejected from the mold? Here, more than for any other variable, ‘rules of thumb’ unfortunately prevail.
Anyone who has spent any time quoting jobs in the plastics industry knows that little, if any, science is brought into the process. For most plastic parts, approximately half of the cost is in the raw material and the other half is related to the machine time required to make the part. The mass of the proposed part is relatively easy to determine with current technology, based on the volume and the solid-state density of the specified material. The number of cavities that will be tooled can be specified so that everyone involved in the quoting process is working from the same general parameters. The big variable then becomes the estimated cycle time. If the process involves a new product, the quoting is done from a two-dimensional drawing or a 3D model. But even in a situation where an actual part is available, you can provide this part to five different people in the industry and get five different estimates of the cycle time.
If you inquire of the participants in this exercise as to how they arrived at the cycle time, you will get a lot of answers that fall into the category of rules of thumb. Factors such as wall thickness, flow length, and specified tolerances will likely be mentioned. But the quantitative relationship between these factors and the estimated cycle time will be elusive. Utilities that are used to determine cycle time can be found everywhere, and it can be a fascinating exercise to examine the underlying assumptions that go into them.
A lot of thought has gone into understanding how to calculate cycle time, and some models have been developed that use impressive-looking equations. These expressions include some quantities such as wall thickness, the thermal diffusivity of the material, and the temperature of the melt and the mold. But there is always one factor that is challenging to define and is a favorite candidate for employing rules of thumb. This is the temperature the polymer must reach so that the part can be ejected from the mold.
What exactly is this temperature? Some programs use the deflection temperature under load (DTUL), also often referred to as the heat-deflection temperature (HDT) of the material. This is a curious choice because it assumes that there is a scientific relationship between the ejection temperature and the DTUL. But if we inquire about the origin of such a relationship, the picture gets a little murky. Ask most people in the industry about the significance of the DTUL and you will get an answer that bears very little resemblance to the true picture.
A reading of the ASTM or ISO method used to measure the DTUL will show that it is the temperature at which a certain deflection is obtained while placing a sample of a very specific and regular geometry under a constant stress. A flex bar is mounted on a three-point bending fixture and the specified stress is applied to the center of the bar. The sample is then heated at a rate of 2° C/min until the required deflection is attained. Since stress divided by strain is the modulus of the material, another way of stating this result is to say that the DTUL is the temperature at which a material achieves a certain modulus.
In 1978, Michael Takemori presented a paper at the SPE ANTEC where he calculated the modulus associated with the DTUL. As most people who have looked at a data sheet know, DTUL can be measured at a stress of 66 psi (0.455 MPa) or 264 psi (1.82 MPa). The ISO method rounds off this higher stress to 1.80 MPa and then adds a third stress level of 1160 psi (8.00 MPa). The modulus associated with 66 psi stress was calculated by Takemori to be 29 ksi (200 MPa) while the modulus associated with the 264 psi stress was calculated to be 116 ksi (800 MPa).
Takemori did not comment on the higher stress of 1160 psi introduced by ISO because it did not exist at the time he wrote his paper. But if it had, he could have easily shown that the associated modulus would have been approximately 510 ksi (3520 MPa).
Which modulus and DTUL stress level should be used for estimating ejection temperature, and why? And what are the chances that a property (DTUL) that has nothing to do with the engineering properties of a polymer is somehow related in a scientific way to the temperature at which a part molded from that material can be ejected without undergoing an unacceptable degree of post-mold distortion?
Takemori went on to show that the DTUL test incorporates a measurement of short-term creep. The sample is placed under constant stress for the duration of the test. This test may last anywhere from 30 min for a material such as a PP copolymer to over 2 hr for a reinforced PEEK or PEK. For the entire duration of that test, the sample is under constant stress and the measured deflection is therefore continually increasing independent of the effects of the increasing temperature. This means that if the sample is left under stress for a sufficient period of time, it will deflect the required amount to signal failure without any need to increase the temperature of the sample.
Takemori also pointed out that as the material temperature increases, the dimensions of the sample increase due to thermal expansion. This introduces a countering influence into the mix that actually pushes on the device used to measure the deflection, prolonging the test.
It has also been noted that the level of molded-in stress in the specimen influences the temperature at which the DTUL is measured. Compression molded samples contain less internal stress than injection molded ones and therefore register a higher DTUL. Samples that have been annealed will also produce a higher measured DTUL for the same reason.
And not all samples are prepared to the same thickness. Thinner samples will deflect at a lower temperature than thicker ones. Given all these variables that are inherent in determining this temperature, how useful can it be as a factor in an equation?
Even if we were to assume that there is some solid science behind this, there are some glaring problems. These are most readily observed in soft, flexible materials. Polyethylene, some polypropylenes, most elastomers, and even PTFE do not have a measurable DTUL because they do not exhibit a modulus high enough to bear the specified stresses prescribed by the test method without immediately deflecting to the degree that signals the conclusion of the test. In order to measure the DTUL of these materials it would be necessary to cool the material below room temperature, allowing the material to stiffen to a point where the test could be started. The result would be a “heat” deflection temperature at some point below room temperature. Therefore, if we use the DTUL as the ejection temperature, these materials would have to be cooled to some very low temperature before the mold could be opened and the part ejected.
This is just the beginning of the problem associated with the way we propose to “calculate” the cycle time of a part. In the next article we will look at how we treat temperature in our equations. We will also explore further some adjustments made to the use of DTUL and review some alternative approaches.
ABOUT THE AUTHOR Mike Sepe is an independent, global materials and processing consultant whose company, Michael P. Sepe, LLC, is based in Sedona, Ariz. He has more than 40 years of experience in the plastics industry and assists clients with material selection, designing for manu- facturability, process optimization, troubleshooting, and failure analysis. Contact: (928) 203-0408 • mike@thematerialanalyst.com.
Related Content
How to Set Barrel Zone Temps in Injection Molding
Start by picking a target melt temperature, and double-check data sheets for the resin supplier’s recommendations. Now for the rest...
Read MoreHot Runners: A View from the Bottom Up
Addressing hot-runner benefits, improvements, and everyday issues from the perspective of decades of experience with probably every brand on the market. Part 1 of 2.
Read MoreHow to Optimize Pack & Hold Times for Hot-Runner & Valve-Gated Molds
Applying a scientific method to what is typically a trial-and-error process. Part 2 of 2.
Read MoreThe Effects of Temperature
The polymers we work with follow the same principles as the body: the hotter the environment becomes, the less performance we can expect.
Read MoreRead Next
People 4.0 – How to Get Buy-In from Your Staff for Industry 4.0 Systems
Implementing a production monitoring system as the foundation of a ‘smart factory’ is about integrating people with new technology as much as it is about integrating machines and computers. Here are tips from a company that has gone through the process.
Read MoreWhy (and What) You Need to Dry
Other than polyolefins, almost every other polymer exhibits some level of polarity and therefore can absorb a certain amount of moisture from the atmosphere. Here’s a look at some of these materials, and what needs to be done to dry them.
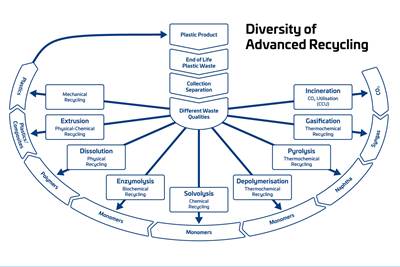
Read MoreAdvanced Recycling: Beyond Pyrolysis
Consumer-product brand owners increasingly see advanced chemical recycling as a necessary complement to mechanical recycling if they are to meet ambitious goals for a circular economy in the next decade. Dozens of technology providers are developing new technologies to overcome the limitations of existing pyrolysis methods and to commercialize various alternative approaches to chemical recycling of plastics.
Read More.jpg;width=70;height=70;mode=crop)