Understanding Viscosity in Extrusion
Both the power-law coefficient and the consistency index must be considered to calculate viscosity.
Viscosity for non-Newtonian polymers is a combination of increasing temperature and shear rate, as described by the following relationship:
η = mγn-1
where viscosity (η) equals consistency index (m) times the shear rate (γ) to the power law index (n) minus 1.
Generally, only rheology experts discuss the effects of the consistency index. The consistency index, or viscosity change with increasing temperature, is largely dependent on the energy input to the polymer by shear from the screw rotation. That is, as the shearing raises the polymer temperature by viscous dissipation or conversion of mechanical power to temperature, the viscosity additionally decreases due to the higher temperature and adds to the shear thinning. The consistency index describes that rate of decrease due to increased temperature.
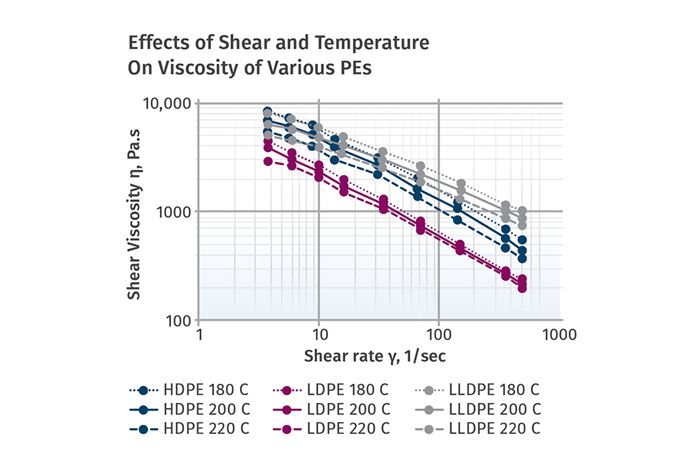
The shear-rate curves in the accompanying graph illustrate the effects of both shear and temperature on viscosity. The individual curves are due to shearing alone, while the spacing between the lines is the temperature effect on viscosity.
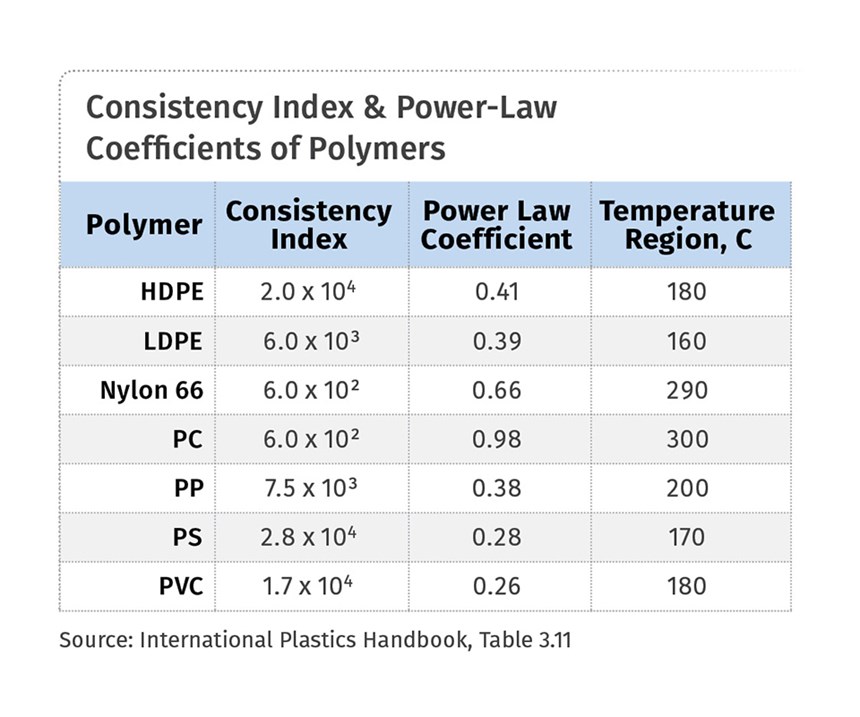
The accompanying table shows values of the consistency index and the power -law coefficient for several common polymers at temperatures in their processing range.
The shear-thinning characteristics of various polymers are often categorized solely by the power-law coefficient, but the consistency index can have just as significant effect on the final viscosity and has to be considered. As the list of polymers in the table shows, the calculated viscosities from the chart at shear rates of 100 sec-1 do not fall in the same order as the power-law coefficients because of that consistency-index effect.
As a result, two polymers of similar melt index or melt flow can have vastly different viscosities at the elevated shear rates during processing. Melt-index and melt-flow measurements by capillary rheometer are at very low shear rates, where shear thinning is almost non-existent. Due to the multiplying effect of power-law coefficient and consistency index, an HDPE and a PP at identical shear rates and slightly different temperatures can have a difference in viscosity where the HDPE is three times as viscous as the PP. This means that the melt temperature of the HDPE on the same screw design is going to be much higher than the PP.
Use of the simple viscosity calculation can greatly assist in analysis of extruder power requirements, melt temperature and polymer flow for different polymers without the use of shear-rate/viscosity graphs
Interestingly, some polymers can reach a near autogenous or adiabatic shear rate where the viscosity drops proportional to the shear rate or screw speed such that further heating through viscous dissipation is minimized and the power-requirement increases only a small amount. For example, I have processed PP at 1500 screw rpm with normal melt temperatures, and the increased power requirement remained largely proportional to the output due to the autogenous effect. However, that’s not true of many polymers.
The actual calculation of the motor load using the calculated viscosity is quite complicated and generally requires computer simulation. However, the calculated viscosity can be a useful tool for approximation of the viscosity and the resulting screw power requirements when coupled with the calculations for viscous dissipation of different polymers on single-screw extruders of different sizes and L/D ratios. Power-law coefficient and consistency data can be found on the internet or from the polymer suppliers.
About the Author
Jim Frankland is a mechanical engineer who has been involved in all types of extrusion processing for more than 40 years. He is now president of Frankland Plastics Consulting, LLC. Contact jim.frankland@comcast.net or (724) 651-9196.
Related Content
Die-Lip Adjustment System Relies on Motorized Actuators
Nordson will debut an automated lip adjustment system for its EDI extrusion and fluid-coating dies at the K 2022 trade fair.
Read MoreOMV Technologies Gets New CEO
Kooper brings 33 years of experience in the industrial and consumer packaging industries to OMV--the closed-loop, turnkey, inline extrusion, thermoforming and tooling systems manufacturer.
Read MoreMacro Names Anzini Tech Sales Manages for Southeast
Has worked in technical roles for leading processing companies in his career of 40+ years.
Read MorePTi Makes Changes in Leadership Structure
Moves aimed at bolstering the future of the sheet extrusion manufacturer.
Read MoreRead Next
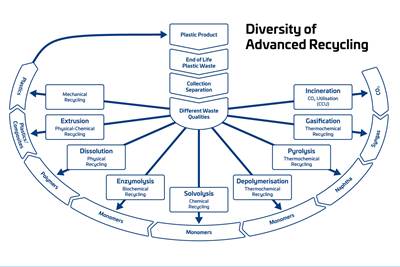
Advanced Recycling: Beyond Pyrolysis
Consumer-product brand owners increasingly see advanced chemical recycling as a necessary complement to mechanical recycling if they are to meet ambitious goals for a circular economy in the next decade. Dozens of technology providers are developing new technologies to overcome the limitations of existing pyrolysis methods and to commercialize various alternative approaches to chemical recycling of plastics.
Read MoreUnderstanding Melting in Single-Screw Extruders
You can better visualize the melting process by “flipping” the observation point so that the barrel appears to be turning clockwise around a stationary screw.
Read MorePeople 4.0 – How to Get Buy-In from Your Staff for Industry 4.0 Systems
Implementing a production monitoring system as the foundation of a ‘smart factory’ is about integrating people with new technology as much as it is about integrating machines and computers. Here are tips from a company that has gone through the process.
Read More
.jpg;width=70;height=70;mode=crop)
















.png;maxWidth=300;quality=90)






.png;maxWidth=970;quality=90)