Simple Scale-Up Calculations for Melting

Scale-up (or -down) of single screws for output involves more than just scaling the metering section. Each screw section must be considered individually and then balanced with the other sections. Adding length to one section subtracts from the others, for example. The metering/pumping section can be analyzed pretty well using the drag-flow/pressure-flow equations, as noted in my column in the January issue.

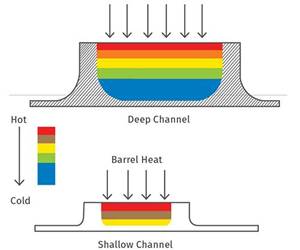
Although some melting occurs in all sections of the screw, the vast majority happens in the compression or tapered-root-diameter section, which is referred to as the melting section. Surprising to many, the effect of conducted heat from the barrel has a relatively small effect on melting, except at very low screw speeds, compared with that caused by viscous dissipation or shearing. Once a melt film forms at the barrel wall, the temperature in the film increases quickly, so that there is little temperature difference to transfer the heat from the barrel to the polymer. Additionally, the polymer itself is an excellent insulator, resisting heat transfer into the unmelted polymer below the melt formed at the barrel wall. Steel, for example, is 130 times as conductive as LDPE. With the same screw geometry, polymer, and peripheral screw speed, the melting rate thus is largely proportional to the area of unmelted polymer, or solid bed, in contact with the barrel for melting by viscous dissipation or shearing.

Determining the melting rate for a conventional flighted screw so that a melting length and taper angle can be determined requires very complex and lengthy analysis. A simpler approach may be used for many scale-up requirements. This approach has been found to give good results when an existing screw with satisfactory performance is being scaled to another size.

In their book, Engineering Principles of Plasticating Extrusion, Zhev Tadmor and Imrich Klein showed the average rate of melting in a tapered channel to be:

ω = (ΦW^0.5)/(2-(A/ψ))

Translating that equation into words: The rate of melting per down-channel distance in a tapered channel is the melting rate multiplied by the square root of the solid-bed width, divided by the quantity two minus the taper rate, divided by the unit melting rate per rate of mass flow per unit channel depth. Despite that complexity, all the data to fill in for Φ, A, and ψ in this equation is available or relatively easily calculated, except “W,” which is the width of the solids in the channel that is in contact with the barrel. Determining the width of solids in contact with the barrel at any one location is a particularly difficult analysis and is mostly a matter of estimates or analysis of precise pressure data at positions along the melting section.

As shown in the accompanying illustration, the channel depth is gradually reduced in the melting section, exerting pressure on the melted and unmelted polymer in the channel. As a result, the solid and melt generally do not move down the channel at the same velocity. Additionally, the relative channel volume is changing due to the compression in the channel. Melting rate is largely unaffected by the channel depth, but very closely related to barrel area in contact with the solids. Consequently, the rate of melting is not directly related to the flow rate or output.

You can use a simplified approach to determine the area of solid contact, which does not actually calculate the melting rate, but only compares the melting performance of one screw to another. Of course, this applies only to processing the same polymer. If the first screw is operating satisfactorily with suitable melt temperature, stability, melt quality and screw life, then a second screw size can be scaled with good results. The same general screw geometry must, of course, be adhered to for this to work satisfactorily. It’s also advisable to limit the scale-up to as small a diameter change as possible.

The ratio of the diameters squared with the same channel depths describes the change in output in the metering section (D2/D1)² for two different screw sizes having the same channel depth and geometry. However, in order to maintain similar melt quality and melt temperature, the channel depth ratio needs to be scaled up by a second ratio. I have typically used (D2/D1)^0.7 as a general scale-up factor with good results, as noted in a previous article. Since the channel area is naturally the ratio of the square of the diameters when changing screw size, if the flight pitch and flight width are kept proportional, the increase in melting length required becomes largely proportional to the increase in depth of the metering section or (D2/D1)^0.7. This means the scale-up in output should be roughly proportional to the scale-up in melting area or [(D2/D1)² × (D2/D1)^0.7]. That can be measured in helical length or simply times the number of flights at the same helix angle. For example, when scaling from a 4.5-in. to a 6-in. screw, the new melting length can be approximated as:

(6.0/4.5)^0.7 = 1.223 × the previous number of flights.

For barrier screws, determining “W” (solid-bed width) is simplified. The main channel is expected to stay essentially full of solids, and the melt is dragged across the barrier into the melt channel as it is formed (assuming the first screw is well designed). This largely eliminates the complex calculation of the varying solid-bed width and an appropriate taper angle or compression rate for the melting section and allows for more accurate scale-up of barrier screws using the simplified melting calculations.

Although certainly not a rigorous analysis, these approximations have worked well across hundreds of screw scale-ups (and -downs) once a good design is found with good results, thus saving a lot of time. Even if you are not designing a new screw, but just evaluating several different screws, it’s a handy reference point

ABOUT THE AUTHOR: Jim Frankland is a mechanical engineer who has been involved in all types of extrusion processing for more than 40 years. He is now president of Frankland Plastics Consulting, LLC. Contact jim.frankland@comcast.net or (724) 651-9196.