Part 5: Heat Deflection Temperature vs. Dynamic Mechanical Analysis

Before we leave this topic, let’s discuss just what is being measured when we conduct a DMA scan. In polymer textbooks DMA is covered in very technical terms accompanied with a lot of math. This works for the very small segment of the industry that is comfortable with such a treatment. In my experience, none of these people are designing parts and specifying the materials from which they should be made. (See also Parts 1, 2, 3  and 4 of this series in January, February, March and April issues.)

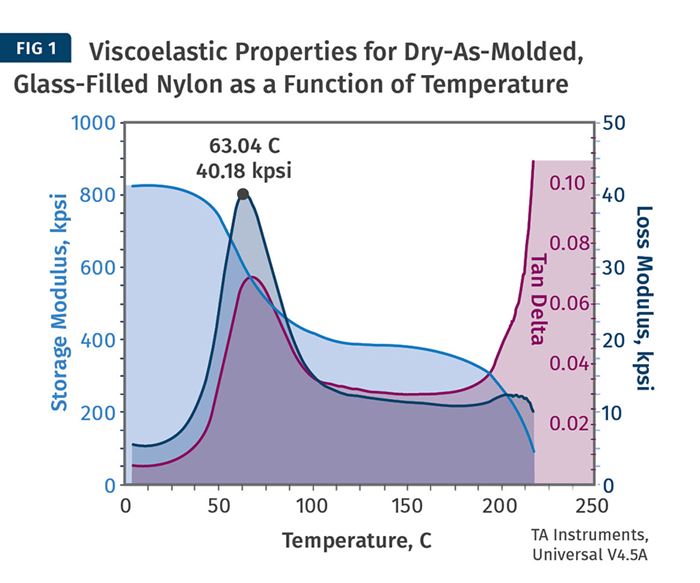
So, let’s see if we can bring it to a practical level using the DMA results for the glass-filled nylon material in Fig. 1. This is a graph we also showed in last month’s article. DMA essentially resolves the complex response that we call the modulus into two components, the elastic modulus and the viscous modulus. Today’s instruments are equipped with a variety of fixtures that can generate the data in tension, flexure, compression, torsion, and shear, so the type of modulus being measured will depend mode of stress employed.

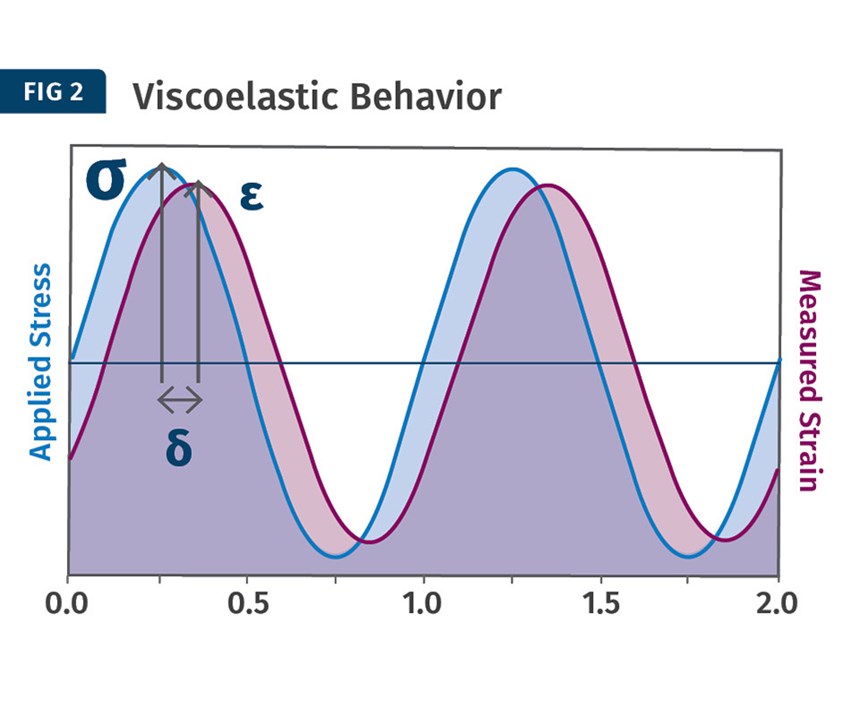
But regardless of the manner in which the stress is generated, the principle of DMA remains the same. A periodic, sinusoidal stress is applied to the sample by a motor and the strain is measured by a transducer. And in this process the real power of DMA becomes apparent. Because in viscoelastic materials there is a delay between the time that the stress is applied and the time that the strain is detected. This phase lag is known as delta (d). Figure 2 shows this relationship.

In a classical stress-strain test, the modulus is calculated as the stress divided by the strain. It is assumed that the stress and the strain are occurring simultaneously. But the DMA test shows that this is not the case. Knowing the value for delta, it becomes possible to calculate the elastic and viscous modulus. The appropriate equations appear below.

 

Elastic Modulus: E′ = (sigma/epsilon) cos delta​​​​

Viscous Modulus: E″ = (sigma/epsilon) sin delta​​​

 

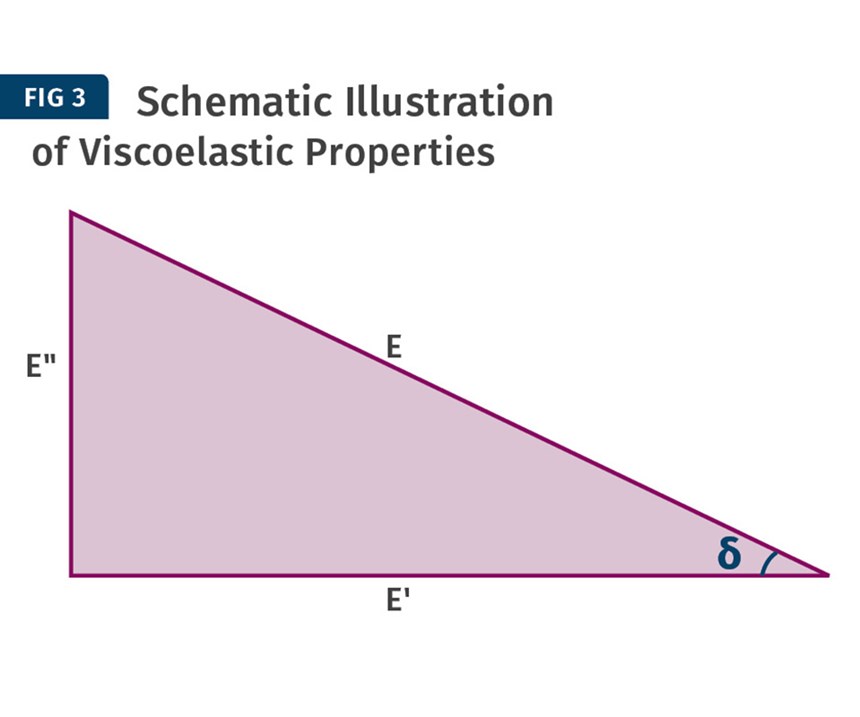
When we square these two terms, add them together, and then take the square root of the resulting sum, we end up with the modulus that most of us are familiar with, what is referred to as the complex modulus and that many equate to Young’s modulus. Therefore, the complex modulus can be thought of as the hypotenuse of a right triangle while the elastic and viscous modulus represent the other two sides, as shown in Fig. 3. The tangent of delta then becomes the ratio of E″/E′, or a kind of index of viscoelasticity.

Now for some good news. For most rigid and semi-rigid polymers at room temperature, the value for tan delta is less than 0.02. This would mean that if the long side of the triangle (E′) in Fig.  3 is 50, then the short side (E″) would be 1 and when you do the math you find that the value for E is 50.01. In other words, at room temperature the elastic modulus and the complex modulus for most materials agree to within one part in 5000 and therefore can be used interchangeably. But if we refer to Fig. 1, we can see that these properties change with temperature and the relationships are not always so straightforward.

Between 50 C and 110 C (122-230 F) the elastic modulus of the glass-filled nylon declines by approximately 50%. This is typical behavior for a highly fiber-reinforced, semi-crystalline polymer. Just as important, as the elastic modulus declines, the viscous modulus rises to a local maximum at a peak temperature of 63 C (145.4 F), which by convention is taken as the glass-transition temperature. Even with all of this sophistication, we can see that trying to define the glass transition as occurring at a specific temperature is a gross oversimplification. It is a relaxation process that unfolds over a temperature range.

But with the availability of the graph we can see in detail how the material is changing. Since tan delta is the ratio of these two moduli, it makes sense that this property will also increase to a local maximum. For this material the value at this peak is approximately 0.07 based on a viscous modulus of 40 ksi and an elastic modulus of 570 ksi. Even under these conditions the elastic and the complex modulus will give good agreement. But now the difference is one part in 400, not 5000. The importance of this change becomes much more apparent when we compare the creep or fatigue resistance of the material at these two temperatures and find that we lose a significant degree of performance at the higher temperature.

We do not even need to compare the material properties at these two temperatures. Instead, we can let nature do the work. Most people who work with nylons know that while they are rigid and perhaps somewhat brittle when just molded, over time they become tougher and more flexible due to their ability to absorb moisture from the atmosphere. This change in performance is driven by a decline in the glass-transition temperature to room temperature or slightly below. In other words, that higher tan delta value shifts toward room temperature. While most of us are familiar with the loss in strength and modulus that comes with this process, few are aware that fatigue life can decline by a factor of over 200. Such is the importance of viscoelasticity.

The reason for this is actually quite simple. The modulus provides information on how a material will respond to an applied stress, and we have already shown that the elastic modulus is quantitatively comparable to the modulus that we traditionally measure. But the viscous modulus captures how a material will recover once that applied stress is removed and also provides information about how rapidly the material will deform over time while under that applied stress. This is the essence of understanding the full spectrum of a material’s behavior under whatever real-world conditions anyone might propose.

We have come a long way from what HDT can provide. The challenge will be to make the availability of DMA data commonplace so that the enhanced understanding that comes with increased exposure to this information can begin to replace our reliance on meaningless single-point data like HDT. It takes time to gain a full understanding of the power of the enhanced characterization tools that are available to us today. The sooner we start, the better for the industry and all of its customers.

ABOUT THE AUTHOR: Mike Sepe is an independent, global materials and processing consultant whose company, Michael P. Sepe, LLC, is based in Sedona, Ariz. He has more than 40 years of experience in the plastics industry and assists clients with material selection, designing for manufacturability, process optimization, troubleshooting, and failure analysis. Contact: (928) 203-0408 • mike@thematerialanalyst.com.